Cztery mile od wielkiej świątyni Angkor Wat, głęboko w kambodżańskiej dżungli, otworzyłem drzwi prowizorycznej szopy z falistym blaszanym dachem i wszedłem do zakurzonego pokoju pomalowanego na jasnoszary kolor. Tysiące kawałków i kamiennych płyt pokrywało brudną podłogę: roztrzaskane głowy posągów khmerskich królów i hinduskich bogów, połamane nadproża i framugi drzwi z opuszczonych świątyń, pozostałości stel ze starożytnym pismem. Po latach poszukiwań w końcu tu przybyłem, mając nadzieję znaleźć pojedynczą kropkę wykutą w czerwonawym kamieniu, skromny znak o niewiarygodnym znaczeniu, symbol, który stałby się fundamentem naszego systemu liczb - naszym pierwszym zero.
To miłość na całe życie doprowadziła mnie do tego progu. Dorastałem na statku wycieczkowym po Morzu Śródziemnym, który często zawijał do Monte Carlo, i pociągały mnie kuszące liczby na kołach ruletki: połowa z nich czerwona, połowa czarna. Moja fascynacja doprowadziła mnie do kariery matematyka i, zajmując się archeologią matematyczną, wytropiłem wiele starożytnych cyfr, w tym magiczny kwadrat (te tajemnicze siatki liczbowe, w których suma każdej kolumny, rzędu i przekątnej jest taka sama) w drzwiach X-wiecznej świątyni Jain w Khajuraho w Indiach.
Jestem przekonany, że stworzenie liczb reprezentujących abstrakcyjne byty, które nazywamy liczbami, było naszym największym osiągnięciem intelektualnym. Prosty znak „3” reprezentuje wszystkie trio we wszechświecie; jest to cecha „bycia trzema” - odróżniającymi się od „bycia pięcioma” lub „bycia siedmioma”. Cyfry pozwalają nam śledzić dobytek, rejestrować daty, wymieniać towary, obliczać tak dokładnie, że jesteśmy w stanie polecieć na Księżyc i działać na mózg.
Używamy ich z taką łatwością, że bierzemy je za pewnik. Co zaskakujące, nasz system liczbowy został przyjęty na Zachodzie dopiero w XIII wieku po tym, jak włoski matematyk Leonardo z Pizy - lepiej znany jako Fibonacci - wprowadził cyfry do Europejczyków. Nauczył się ich od arabskich kupców, którzy prawdopodobnie adoptowali ich podczas podróży na subkontynent indyjski.

Finding Zero: A Mathematician's Odyssey to Uncover the Origins of Numbers
Wynalazek cyfr jest prawdopodobnie największą abstrakcją, jaką ludzki umysł kiedykolwiek stworzył. Praktycznie wszystko w naszym życiu ma charakter cyfrowy, liczbowy lub ilościowy. Historia, w jaki sposób i gdzie otrzymaliśmy te cyfry, od których tak bardzo polegamy, od tysięcy lat spowita jest tajemnicą. „Finding Zero” to pełna przygód saga o życiowej obsesji Amira Aczela: znaleźć oryginalne źródła naszych cyfr.
KupowaćZe wszystkich cyfr „0” - samodzielnie na zielono na kole ruletki - ma największe znaczenie. Unikalna w reprezentowaniu absolutnej nicości, jej rola jako symbolu zastępczego nadaje naszemu systemowi liczbowemu swoją moc. Umożliwia cykliczne liczenie cyfr, nabierając różnych znaczeń w różnych lokalizacjach (porównaj 3 000 000 i 30). Z wyjątkiem systemu Majów, którego glif zerowy nigdy nie opuścił obu Ameryk, nasz jedyny znany jest z cyfrą zero. Babilończycy mieli znamiona nicości, mówią niektóre relacje, ale traktowali to przede wszystkim jako interpunkcję. Rzymianie i Egipcjanie też nie mieli takiej liczby.
Krąg zapisany w świątyni w Gwalior w Indiach, pochodzący z IX wieku, był powszechnie uważany za najstarszą wersję zera w naszym systemie, hindusko-arabską. W tym czasie handel z imperium arabskim łączył Wschód i Zachód, aby mógł pochodzić z dowolnego miejsca. Dążyłem do starszego zera, szczególnej instancji opowiadającej się za wschodnim pochodzeniem.
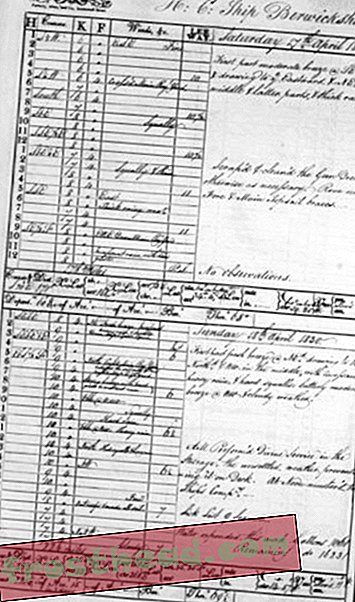
Znaleziony na kamiennej steli został udokumentowany w 1931 r. Przez francuskiego uczonego George'a Coedèsa. Napis, któremu przypisano etykietę identyfikacyjną K-127, brzmi jak rachunek sprzedaży i zawiera odniesienia do niewolników, pięciu par wołów i worków białego ryżu. Chociaż niektóre pisma nie zostały odszyfrowane, napis wyraźnie nosił datę 605 w starożytnym kalendarzu, który rozpoczął się w roku 78 ne. W ten sposób datowano go na 683 rne. Dwa wieki starszy niż ten w Gwalior, był wcześniejszy niż szeroki Arabski handel. Ale K-127 zniknął podczas rządów terroru Czerwonych Khmerów, gdy celowo zniszczono ponad 10 000 artefaktów.
Swoją obsesję na punkcie znajdowania tego najwcześniejszego zera opisuję w mojej nadchodzącej książce Finding Zero . Spędziłem niezliczone godziny, przeglądając stare teksty w bibliotekach od Londynu po Delhi, wysyłając e-maile i dzwoniąc do każdego, kto mógłby znać kogoś, kto mógłby mi pomóc zlokalizować K-127. Odbyłem kilka nieudanych podróży do Kambodży, wydając znaczną część własnych pieniędzy. Na granicy poddania się otrzymałem grant od Fundacji Alfreda P. Sloana i ruszyłem naprzód. Dyrektor generalny Kambodży w Ministerstwie Kultury i Sztuk Pięknych, Hab Touch, skierował mnie do szop w Angkor Conservation, miejscu renowacji i przechowywania zamkniętym dla publiczności. Kiedy dwa razy mnie odmówiono, Touch łaskawie zadzwonił i na początku stycznia 2013 roku zostałem zaproszony. Wciąż nie wiedziałem, czy K-127 przeżył.
A jednak w ciągu dwóch godzin koło ruletki obróciło się na moją korzyść. Moje oko złapało kawałek taśmy z wypisanym ołówkiem „K-127”, a potem rozpoznałem tę pojedynczą kropkę na płycie o wymiarach 3 na 5 stóp, nienaruszoną, ale z grubsza przerwaną na górze. Byłem podniecony. Nie odważyłem się dotknąć kamiennej powierzchni z obawy, że mogę ją skrzywdzić.
Od tamtego losu zastanawiałem się nad wyczynem, który przyniósł nam cyfry, tym razem nie zastanawiając się, gdzie i kiedy, ale jak? Zadałem dziesiątkom matematyków długo dyskutowane pytanie: Czy liczby zostały odkryte czy wynalezione? Większość uważa, że liczby istnieją poza ludzkim umysłem. W przeciwieństwie do IX Symfonii Beethovena nie wymagają one ludzkiego twórcy. Tym, co dało liczbom ich moc, był sam ich nazywanie i zapisywanie. Pracuję teraz z urzędnikami z Kambodży, aby przenieść K-127 do muzeum w Phnom Penh, gdzie szeroka publiczność może docenić niesamowite odkrycie, które reprezentuje.