Kiedy większość z nas widzi maszynę do ciągnięcia po taffy odjeżdżającą na turystycznej promenadzie, myślimy o słodkim, słodkim cukrze. Jean-Luc Thiffeault myśli o słodkiej, słodkiej matematyce. Jako matematyk stosowany na University of Wisconsin-Madison, Thiffeault jest szczególnie zainteresowany sposobem mieszania materiałów takich jak taffy: w maszynie cukierki są rozciągane i składane w celu włączenia powietrza i rozwinięcia lekkiej, nadającej się do żucia tekstury. W miarę wyciągania pierwotny prostokąt tafty jest coraz bardziej rozciągany - jego długość rośnie wykładniczo o ten sam współczynnik za każdym razem. Ten współczynnik rozciągliwości interesuje Thiffeault.
powiązana zawartość
- Czekolada w stopie, żelki z nadrukiem 3D i inne fascynujące patenty na cukierki
Kiedy osoba ciągnie Taffy, zazwyczaj bierze kawał cukierka i naciąga go na haczyk, łącząc oba końce razem. Następnie wezmą ten złożony kawałek i rozciągną go ponownie na haku, podwajając długość i tak dalej. Innymi słowy, „ludzki sposób na zrobienie tego jest mnożnikiem 2”, mówi Thiffeault. Mechaniczne ściągacze mogą radzić sobie lepiej, często dając większe, egzotyczne liczby nieracjonalne jako czynniki rozciągające.
Okazuje się, że ściąganie taffy może być modelowane przez abstrakcyjne pole matematyki znane jako dynamika topologiczna, zasadniczo badanie długoterminowych zmian na dużą skalę w czasie w przestrzeni matematycznej. (Jeśli słowo „topologia” brzmi znajomo, ostatnio pojawiło się w wiadomościach w ramach tegorocznej Nagrody Nobla w dziedzinie fizyki.) Ta sama matematyka, która opisuje ściąganie tafty ma również poważniejsze zastosowania: wiele procesów przemysłowych, w tym dmuchanie szkła i przygotowywanie leków, wymaga lepkie płyny do mieszania w sposób bardziej podobny do wciągania toffi niż mieszania śmietanki do kawy. „Jeśli próbujesz mieszać naprawdę lepkie rzeczy, takie jak pasty przemysłu farmaceutycznego, nie możesz ich po prostu wstrząsnąć”, mówi Thiffeault. „To nie jest jak mieszanie farby.”
Thiffeault od dawna rozumiał ściąganie tafty jako przykład lepkiego mieszania, ale dopiero niedawno zagłębił się w historię ściągaczy tafli, aby odkryć ich matematyczne tajemnice. Rezultatem tej wycieczki do patentów historycznych jest jego najnowszy artykuł „Matematyczna historia ściągaczy tafty”, opublikowany na serwerze preprint arXiv w lipcu.
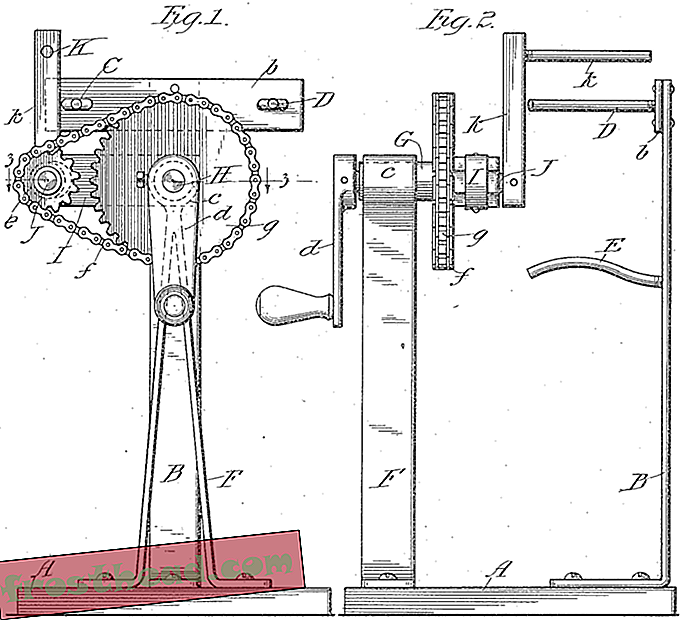Obraz z patentu na maszynę taffy z 1916 r., Który pojawia się w badaniu Thiffeault. W szczególności obszarem, który doprowadził do jego głębokiego nurkowania z ściągaczami taffy, jest badanie tak zwanych mapowań pseudo-Anosov. Pseudo-Anosow to fantazyjny sposób opisywania procesu, w którym dwuwymiarowy kształt jest rozciągany wykładniczo w jednym kierunku, podczas gdy kurczy się w drugim. Matematycznie badanie mapowań pseudoanosowskich jest stosunkowo nowe. „W latach 70. i 80. ludzie bardzo starali się znaleźć przykłady” - mówi Thiffeault. Jak na ironię, byli tam cały czas w patentach dla ściągaczy tafty. „Ponieważ matematycy nigdy nie patrzyli na tę literaturę, nigdy nie wiedzieliby, że istnieją” - mówi.
Podczas gdy przeczesywał patenty ściągacza tafty, Thiffeault natknął się na legalną bitwę, która dotarła aż do Sądu Najwyższego. Kwestią sporną w sprawie Hildreth przeciwko Mastoras z 1921 r . Było to, jak szeroko należy interpretować patent z 1900 r. Na ściągacz w kształcie tafty. To znaczy: czy późniejszy model wykonany przez kogoś innego był jedynie drobnym ulepszeniem, czy może było to inne urządzenie? Istotną częścią argumentu było to, jak różny był patent z 1900 r. Od poprzednika z 1893 r. (Który prawdopodobnie nigdy nie został wyprodukowany). Opinia sądu, której autorem jest naczelny sędzia William Howard Taft, „wykazuje głębokie zrozumienie dynamiki topologicznej”, pisze Thiffeault w swoim artykule.
Sąd uznał, że wcześniejsze urządzenie, które miało tylko dwa haczyki, nie mogło rozciągać tafi w wykładniczym stopniu wymaganym do skutecznego tworzenia słodyczy. Opinia Tafta stwierdza:
Za pomocą tylko dwóch haczyków nie można było docierać cukierka, ponieważ nie było trzeciej szpilki do ponownego włączenia cukierka, gdy był on trzymany między pozostałymi dwoma szpilkami. Ruch dwóch kołków w koncentrycznych okręgach może go nieco rozciągnąć i mieszać, ale nie pociągnie go w sensie sztuki.
Thiffeault pisze: „Opinia Sądu Najwyższego pokazuje fundamentalny pogląd, że do wytworzenia pewnego rodzaju szybkiego wzrostu potrzebne są co najmniej trzy pręty”.
Thiffeault twierdzi, że obecnie są w użyciu dwa standardowe ściągacze w kształcie tafty, jeden z trzema prętami i jeden z czterema. Zdarza się, że mają ten sam współczynnik rozciągania. Jest to związane z tak zwanym współczynnikiem srebra, 1+ √2 lub około 2, 414, nieco mniej świecącym kuzynem bardziej znanego złotego współczynnika.
Interesujący jest fakt, że dwa standardowe ściągacze w kształcie tafty rozciągają się ze stosunkiem srebra, ponieważ stosunek srebra jest - w dokładnym sensie matematycznym - optymalny. Jednak Thiffeault ostrzega, że niełatwo jest uszeregować różne ściągacze tafi, nawet jeśli znasz ich czynniki rozciągające: „Jest w tym aspekt jabłek i pomarańczy, który jest dość trudny do obejścia” - mówi. Jeden ściągacz może mieć więcej prętów i powrót do stanu początkowego może trwać dłużej niż inny, lub może wymagać większego momentu obrotowego lub bardziej skomplikowanej przekładni. Tak więc, chociaż matematyka daje pewien wgląd w to, jak dobrze ciągną za sobą ściągacze tafi, to nie opowiada pełnej historii.
Badania Thiffeaulta dotyczące ściągaczy taffy zainspirowały go i jego studenta, Alexa Flanagana do zbudowania własnego modelu. Chcieli sprawdzić, czy mogą zwiększyć wydajność bez znacznej zmiany biegów, i ostatecznie stworzyli nowatorski ściągacz 6-prętowy oparty na przekładni standardowego ściągacza 4-prętowego. „Powodem, dla którego byliśmy w stanie to zrobić, jest fakt, że teraz mamy matematykę” - mówi Thiffeault. Mogliby szeroko modelować maszynę na komputerze i ominąć wiele prób i błędów z prawdziwymi urządzeniami fizycznymi, które wcześniej musieli zrobić wynalazcy. 6-prętowe urządzenie, które wciąż jest tylko prototypem, rozciąga tafi mniej więcej dwa razy więcej niż standardowe ściągacze w każdym cyklu.
Jak dotąd producenci ściągaczy tafli nie biją dokładnie drzwi Thiffeaulta, aby uzyskać jego porady dotyczące optymalizacji ich projektów - Big Taffy najwyraźniej jest zadowolony ze swojego elastycznego status quo - ale ma nadzieję, że jego metody mogą przynieść efekty w innych branżach. Oprócz dmuchania szkła, jednym logicznym miejscem optymalizacji mieszania jest przemysł farmaceutyczny. W końcu mieszanie witamin i leków wymaga niezwykle wysokiej kontroli jakości: producenci są „gotowi zapłacić dużo pieniędzy za idealne mieszanie”, ponieważ „nie tolerują jednej złej multiwitaminy na 1000”, mówi Thiffeault. Więc pewnego dnia farmaceuci mogą słodko wykrzyczeć oddanych temu porywaczom.
Z drugiej strony może to być trochę trudne.
