14 marca to nie jest regularny Dzień Pi w tym roku. Entuzjaści matematyki na całym świecie świętują to wydarzenie jako Dzień Ostatecznego Pi, ponieważ data będzie odpowiadać pierwszym pięciu cyfrom pi (3.1415), a nie tylko trzem pierwszym. Ta matematyczna zbieżność nie pojawi się ponownie przez stulecie, 14 marca 2115 r.
powiązana zawartość
- Świat jest pełen kół
Zdefiniowana jako stosunek obwodu koła do jego średnicy, pi ( π ) jest zarówno liczbą transcendentalną, jak i irracjonalną, co oznacza, że nigdy nie można go zapisać jako stosunek dwóch liczb całkowitych i trwa w nieskończoność bez powtarzającego się wzoru. Pi nie jest jedyną liczbą niewymierną - na przykład jest też liczba Eulera (e) i złoty współczynnik ( φ lub phi). Mario Livio, astrofizyk z Space Telescope Science Institute w Maryland, nadal jednak jest źródłem fascynacji, ponieważ jego pochodzenie można łatwo wyjaśnić.
„Każdy może zrozumieć, jak powstaje pi. Wszystkie pozostałe liczby są bardziej złożone. Na przykład liczba phi obejmuje określony podział linii, a liczba e wymaga znajomości logarytmu - mówi Livio, autor książki Czy Bóg jest matematykiem?
Inną dużą zaletą pi jest to, że ma niesamowity talent do pojawiania się w formułach matematycznych, z których wiele jest ważnych w codziennych procesach, od przetwarzania obrazu po nawigację GPS. Oto tylko niewielka próbka powszechnie używanych formuł, które obejmują pi:
Transformacja Fouriera
To matematyczne narzędzie, nazwane na cześć francuskiego matematyka Jean-Baptiste Josepha Fouriera, rozkłada sygnał na częstotliwości składowe - raczej jak rozbicie akordu muzycznego na nuty składowe. Zasadniczo transformaty Fouriera są idealne do przetwarzania sygnałów opartych na falach, takich jak dźwięk lub światło, i wyszukiwania wzorców. To sprawia, że transformacja Fouriera jest podstawowym narzędziem we współczesnym cyfrowym świecie.
„Jest nazywany najważniejszym algorytmem opracowanym kiedykolwiek przez ludzkość. To może być hiperbola, ale może nie ”- mówi Glen Whitney, założyciel i dyrektor National Museum of Mathematics w Nowym Jorku. Transformacje Fouriera są używane przez cały czas do czyszczenia obrazów cyfrowych, do automatycznego dostrojenia gwiazd pop oraz do znajdowania odległych planet krążących wokół innych gwiazd. Narzędzie ma również kluczowe znaczenie dla funkcji konwersji głosu na tekst, które są teraz standardem w smartfonach. „Gdy używasz Siri lub Google Now, jednym z pierwszych kroków jest zabranie głosu i wykonanie na nim transformacji Fouriera… okazuje się, że łatwiej rozpoznać samogłoski, kiedy spojrzysz na ich transformacje Fouriera niż na oryginalne sygnały same w sobie - mówi Whitney.
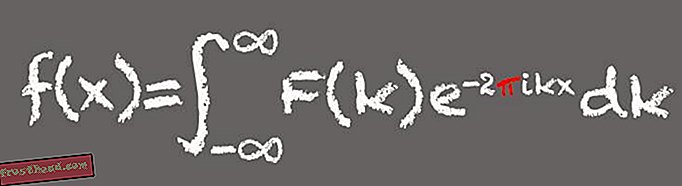 (Ilustracja: Victoria Jaggard)
(Ilustracja: Victoria Jaggard) Pi pojawia się w transformacie Fouriera, ponieważ jedna z części składowych lub wyrażeń formuły jest powiązana z sinusem i cosinusem oraz kątami tworzonymi przez cząstkę poruszającą się po okręgu. „Ilekroć masz formułę dotyczącą okręgów lub kątów, nie będziesz zaskoczony, gdy pojawi się pi”, mówi Whitney.
Zasada nieoznaczoności Heisenberga
Jeden z filarów mechaniki kwantowej, zasada nieoznaczoności Heisenberga stwierdza, że obserwator nie może jednocześnie znać położenia i prędkości cząsteczki subatomowej. Zamiast tego, im dokładniej znana jest pozycja cząsteczki, tym mniej można powiedzieć o jej prędkości.
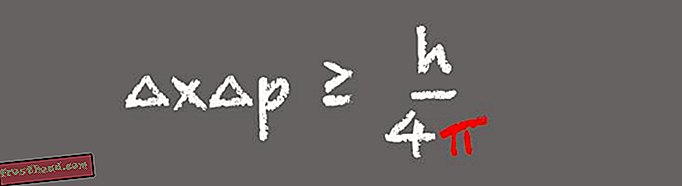 (Ilustracja: Victoria Jaggard)
(Ilustracja: Victoria Jaggard) Pojawienie się pi w zasadzie nieoznaczoności Heisenberga ma sens, gdy uświadomisz sobie, że we wzorze, pozycji i pędzie są transformaty Fouriera względem siebie, mówi Whitney. Zasada nieoznaczoności jest ważna we współczesnym świecie, ponieważ opisuje zachowanie cząstek światła lub fotonów w światłowodowych systemach komunikacyjnych. „Mówi nam to, że nie jesteśmy w stanie poznać zarówno położenia, jak i pędu fotonów z niezwykłą precyzją. Nie można zaprojektować protokołów komunikacyjnych, które naruszają zasadę nieoznaczoności Heisenberga, ponieważ nie będą działać ”.
Prawo Stoke'a
Prawo Stoke'a oblicza siłę potrzebną do poruszenia małej kuli - czyli trójwymiarowego koła - przez lepki płyn z określoną prędkością. Ma zastosowania w dziedzinach od nauk o Ziemi po medycynę.
 (Ilustracja: Victoria Jaggard)
(Ilustracja: Victoria Jaggard) „Prawo dotyczy w szczególności wpływu lepkości na kulę w płynie”, mówi Whitney, i tak zaczyna się pi. Jeśli chodzi o praktyczne zastosowania prawa Stoke'a, nie szukaj dalej niż samochód. „Przez dziesięciolecia firmy upewniały się, że olej silnikowy ma odpowiednią lepkość do twojego samochodu, dosłownie upuszczając serię kulek testowych do oleju i mierząc czas, w którym spadają one z płynu”, mówi Whitney. Obecnie najczęstszym sposobem pomiaru lepkości oleju jest narzędzie zwane wiskozymetrem z rurką kapilarną, nie są potrzebne żadne kule - ale nadal podaje ono wynik w jednostkach miary zwanych centystokami.
Formuła Eulera
Nazwana na cześć szwajcarskiego matematyka Leonarda Eulera, wersja tej formuły, która zawiera pi, gromadzi jedne z najbardziej intrygujących liczb w matematyce w jednym miejscu:
 (Ilustracja: Victoria Jaggard)
(Ilustracja: Victoria Jaggard) „Wszyscy myślą, że to niesamowite. Wszystkie te liczby, które uważamy za wyjątkowe, pojawiają się w jednym pięknym równaniu ”, mówi Livio. Chociaż ta zwięzła formuła może wzbudzić podziw u matematyków, bardziej użyteczna forma równania jest nieco dłuższa:
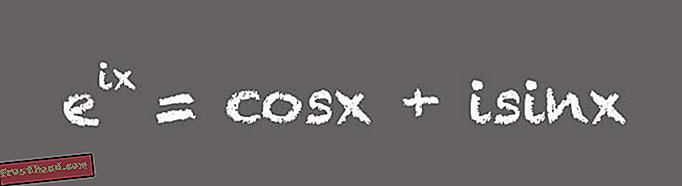 (Ilustracja: Victoria Jaggard)
(Ilustracja: Victoria Jaggard) Whitney mówi, że ta rozpakowana wersja formuły Eulera jest niesamowitym narzędziem. Na przykład jest to ważne przy projektowaniu elektroniki wykorzystującej prąd przemienny lub prąd przemienny. „Formuła Eulera w rozszerzonej formie oznacza, że możesz używać złożonych lub urojonych liczb do analizowania i projektowania obwodów prądu przemiennego” - mówi Whitney. Jest tak, ponieważ w obwodzie prądu przemiennego napięcie jest wielkością, która oscyluje w czasie - zwykle 60 razy na sekundę, na przykład w standardowym zasilaniu elektrycznym w USA. „Pełna wersja formuły Eulera uczy, w jaki sposób możemy wykorzystywać liczby zespolone jako wygodny skrót do modelowania zjawisk oscylacyjnych” - mówi Whitney.
Równania pola Einsteina
Zasadniczy element jego ogólnej teorii względności, równania pola Alberta Einsteina opisują, w jaki sposób grawitacja od masy i energii tworzy krzywiznę czasoprzestrzeni.
 (Ilustracja: Victoria Jaggard)
(Ilustracja: Victoria Jaggard) „Opisanie krzywizny obejmuje geometrię, a ponieważ pierwotna definicja pi pochodzi od geometrii, jej wygląd w tym równaniu nie jest aż tak zaskakujący”, mówi Livio. Oprócz ujawnienia fundamentalnej prawdy o tym, jak działa wszechświat, ogólna teoria względności ma wiele praktycznych zastosowań. Na przykład satelity tworzące globalny system pozycjonowania wykorzystywane do nawigacji byłyby beznadziejnie zsynchronizowane ze sobą, gdyby inżynierowie nie wzięli pod uwagę przewidywanych przez teorię efektów dylatacji czasu.


